시간 복잡도와 Big-O 표기법 정리와 더불어
코테 준비로 사용하는 python 언어에서 자료형별 시간복잡도를 정리하였다.
1. 1. 점근 표기법(Asymptotic notation)
점근 표기법 : 알고리즘의 성능과 효율성을 표기해주는 표기법
여기서 말하는 효율성은 실행시간이 적으냐(=시간복잡도), 메모리를 덜 차지하는지(=공간복잡도)에 걸려있다.
결국 시간복잡도와 공간복잡도를 나타내는 표기법인 셈.
- 시간복잡도(Time Complexity) : 입력된 N의 크기에 따라 실행되는 조작의 수
- 공간복잡도(Space Complexity) : 알고리즘이 실행될 때 사용하는 메모리의 양
점근 표기법에는 대표적으로 대문자 O 표기법, 소문자 o 표기법, 대문자 오메가(Ω) 표기법, 소문제 오메가 표기법(ω), 대문자 세타(Θ) 표기법으로 5가지가 있다.
그러나 이 중 압도적으로 많이 쓰이는 것은 대문자 O 표기법, 즉 Big O 표기법이다.
2. 2. Big-O 표기법(Big-O notation)
Big-O 표기법 : 입력값이 무한대로 향할 때 함수의 상한을 설명하는 수학적 표기 방법
점근적 실행 시간을 표기할 때 가장 널리 쓰이는 수학적 표기 방법이다.
여기서 점근적 실행 시간이란 n이라는 입력값이 무한대로 커질 대의 실행 시간의 추이를 의미한다.
그렇다면 왜 Big-O 표기법을 주로 사용할까?
앞서 말한 점근 표기법을 다시 보자.
- O 표기법 : 알고리즘의 최악의 성능을 표시
- Ω 표기법 : 알고리즘의 최고의 성능을 표시
- Θ 표기법 : 정확한 알고리즘의 성능을 표시
세타 표기법이 이상적이고 정확하지만, 실제로 구하기가 어렵다.
다른 오메가 표기법으로 나타낼 때 최고라고 해도 만약 최악의 경우라면 ? 할 이유가 없다.
결국 우리는 최악의 경우에 어떻게 되는지에 관심이 있기 때문에 빅 오 표기법을 사용한다.
3. 3. Big-O 표기법의 종류

그래프에 나와 있는 시간 복잡도의 성능을 비교하면 다음과 같다.
왼쪽에서 오른쪽으로 갈수록 효율성이 떨어진다.
O(1) < O(log n) < O(n) < O(n * log n) < O(n^2) < O(n^3) < O(2^n) < O(n!)
4.
5. 4. 시간복잡도를 구하는 요령
- 하나의 루프를 사용하여 단일 요소 집합을 반복 : O(n)
- 컬렉션의 절반 이상을 반복하는 경우 : O(n/2) -> O(n)
- 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복할 경우 : O(n+m) -> O(n)
- 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O(n^2)
- 두 개의 중첩 루프를 사용하여 두 개의 다른 컬렉션을 반복하는 경우 : O(n*m) -> O(n^2)
- 컬렉션 정렬을 사용하는 경우 : O(n*log(n))
6. 5. 정렬 알고리즘 비교
| 정렬 알고리즘 | 공간 복잡도 | 시간 복잡도 | ||
| 최악 | 최선 | 평균 | 최악 | |
| 버블 정렬 (Bubble Sort) |
O(1) | O(n) | O(n^2) | O(n^2) |
| 힙 정렬 (Heap Sort) |
O(1) | O(n log n) | O(n log n) | O(n log n) |
| 삽입 정렬 (Insertion Sort) |
O(1) | O(n) | O(n^2) | O(n^2) |
| 병합 정렬 (Merge Sort) |
O(n) | O(n log n) | O(n log n) | O(n log n) |
| 퀵 정렬 (Quick Sort) |
O(log n) | O(n log n) | O(n log n) | O(n^2) |
| 선택 정렬 (Selection Sort) |
O(1) | O(n^2) | O(n^2) | O(n^2) |
| 셸 정렬 (Smooth Sort) |
O(1) | O(n) | O(n log n^2) | O(n log n^2) |
7. 6. 파이썬 자료형 별 시간 복잡도
리스트(List)/튜플(Tuple)

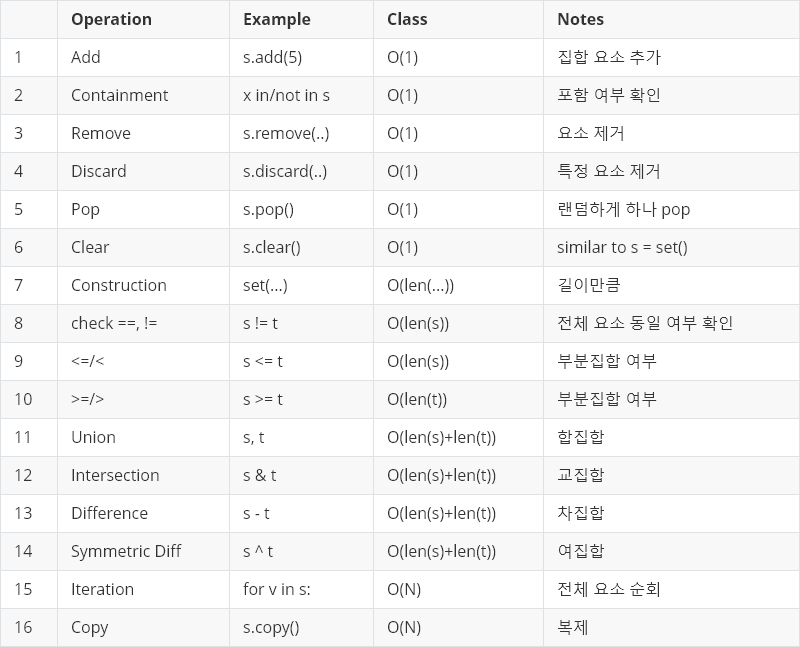
집합(set)
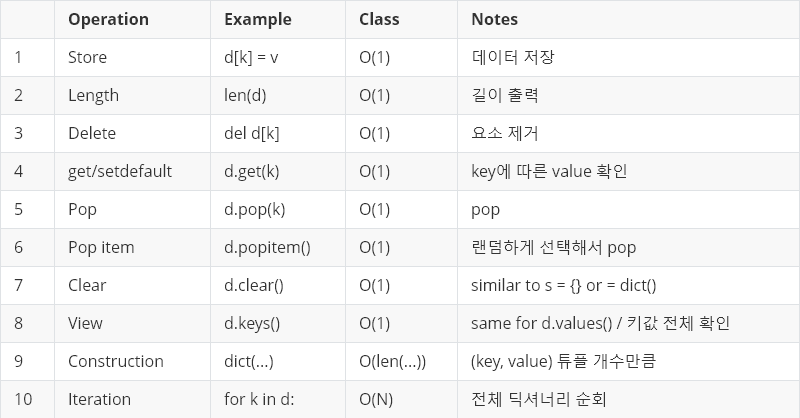
딕셔너리(Dictionary)
8. 참고 자료
https://www.ics.uci.edu/~pattis/ICS-33/lectures/complexitypython.txt
https://blog.chulgil.me/algorithm/
알고리즘의 시간 복잡도와 Big-O 쉽게 이해하기
삼성역에서 택시를 타고 강남역으로 향했는데 30분 걸렸다. 구글에서 알려주는 최단경로로 갔더라면 15분내에 도착할 것이다. 레스토랑을 예약해서 가는 경우라던지 친구와 약속시간을 잡은경
blog.chulgil.me
https://noahlogs.tistory.com/27
빅오 표기법 (big-O notation) 이란
컴퓨터 과학(Computer Science) 에서 알고리즘은 어떠한 문제를 해결하기 위한 방법이고, 어떠한 문제를 해결 하기 위한 방법은 다양하기 때문에 방법(알고리즘) 간에 효율성을 비교하기 위해 빅오(
noahlogs.tistory.com
https://velog.io/@qksud14/Algorithm-BigO
Algorithm(빅오 표기법:Big-O Notation)
Big-O 표기법이란? 알고리즘의 효율성을 수학적으로 표기하는 방식 시간과 공간 복잡도를 표현해 준다.
velog.io
'Algorithm' 카테고리의 다른 글
| [Algorithm][Python3][BOJ 1300] K번째 수 (0) | 2022.02.09 |
|---|---|
| [Algorithm][BOJ 9251] LCS (0) | 2022.02.02 |
| [Algorithm][Programmers] 주식 가격 - python (0) | 2022.01.26 |
| [Algorithm][BOJ 13335] 트럭 - python (0) | 2022.01.25 |
| [Algorithm][BOJ 15565] (Python) 귀여운 라이언 (0) | 2022.01.25 |

